Krafton_jungle 5기 11일차 TIL - 알고리즘 시험, 그래프 자료구조, CS:APP

알고리즘 시험

 

1. 1110 더하기 사이클

저번에 풀이한 방법은 while문을 사용해서 풀었길레 이번엔 재귀를 사용해서 풀이했음.

 

 

2. 1182 부분수열의 합

파이썬 내장 모듈 사용 안하고 풀려다가 시간 엄청 까먹었다...

그냥 모듈 사용하고 3번으로 갈걸

 

3. 1992 쿼드트리

import sys
input = sys.stdin.readline


def solve(x, y, total_length):
	global res
	if total_length <= 0:
		return
	flag = search(x,y,total_length)
	if flag == 2:
		res += "("
		solve(x, y, total_length//2)
		solve(x+total_length//2, y, total_length//2)
		solve(x, y+total_length//2, total_length//2)
		solve(x+total_length//2, y+total_length//2, total_length//2)
		res += ")"
	else:
		res += str(flag)

	

def search(x, y, total_length):
	flag = plate[y][x]
	for i in range(y, y + total_length):
		for j in range(x, x + total_length):
			if plate[i][j] != flag:
				return 2
	return flag


n = int(input())

plate = []
res = ""
for i in range(n):
	string = input().rstrip()
	row = []
	for i in string:
		row.append(int(i))
	plate.append(row)
	
solve(0,0,len(plate))
print(res)

저번에 풀었던 색종이 문제와 크게 다르지 않아 어렵지 않게 풀었다.

 

생각보다 쉬웠지만 결과는 1/3솔... 시간이 조금만 더 있었더라면 하는 아쉬움이 있다.

 

 

그래프

그래프란?	연결되어 있는 원소간의 관계를 표현한 자료구조로, 정점(Vertex)과 각 정점을 연결하는 간선(Edge), 그리고 한 방향으로만 이동할 수 있는 간선인 arc의 집합으로 구성되어 있다. Dgree(차수) 정점에 부속되어있는 간선의 개수
그래프의 종류	무방향 그래프(Undirected graph) 정점을 연결하고 있는 간선의 방향이 없어, 어디로든 이동할 수 있다. 방향 그래프(Directed graph) arc로 구성되어 있어 단방향으로만 탐색이 가능한 그래프 완전 그래프(Complate graph) 모든 정점이 간선으로 연결되어 있는 그래프 가중 그래프(Weight greph) 간선에 가중치를 할당해, 가중치만큼의 이동만 가능한 그래프

 

그래프의 표현 방식

인접행렬

인접 행렬

그래프를 2차원 배열에 저장한다. 부속된 간선을 찾는것은 빠르지만 메모리를 많이 사용한다. 노드 수보다 간선 수가 많은 dense graph이거나 빠르게 부속된 간선을 찾을 때 주로 사용한다. dense graph 란 간선의 수가 최대 간선의 수에 가까운 그래프이다.

 

무방향, 방향 그래프

 

다음과 같은 방향 그래프는 파이썬 코드로 이렇게 구현할 수 있다.

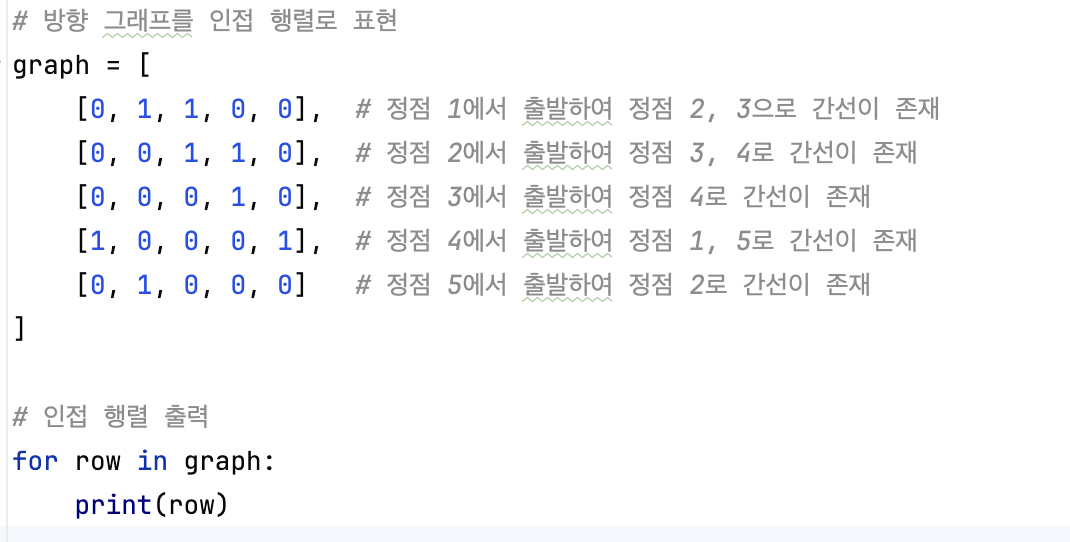
코드를 보면 2차원 배열로 연결된 간선을 직접적으로 선언해줘, 탐색에 용의한 모습을 볼 수 있다.

하지만 N*N 만큼의 메모리를 할당해줘야 함을 알 수 있다.

무방향도 이 형식과 크게 다르지 않다.

 

가중 그래프

위에 있는 그래프에 가중치가 더해진다고 생각해보자.

이는 어떤 방법으로 표현할 수 있을까?

가중 그래프는 다음과 같이 표현할 수 있다. 

표현 방식에 있어 그리 크게 다른점을 볼 수 없다.

 

시간 복잡도

어느 두 정점에 부속된 간선이 있는지 탐색할 경우 - O(n) 인접한 정점찾기 O(n) 공간복잡도 - v*v

 

 

인접 리스트

인접리스트

인접한 정점을 연결 리스트로 표현 연결된 간선에 대한 값만 저장. 메모리 적게씀 간선 수보다 노드 수가 많은 spare graph에 주로 사용 정점은 배열에 저장하고 각 정점에 인접한 정점은 연결리스트로 관리 (해시의 체이닝이 생각난다)

 

방향, 무방향 그래프

우선은 파이썬의 배열을 사용해 링크드 리스트를 대체했지만 이런식으로 구현한다고 보면 된다.

 

가중 리스트

가중 그래프는 가중치를 저장하는 필드값을 따로 추가해주는 모습을 확인할 수 있다.

 

시간 복잡도

특정 간선을 탐색한다 - O(n) 인접한 정점을 탐색한다 - O(n) 공간 복잡도 - O(노드 + 간선)

 

Walk

walk란?	walk는 노드를 탐색하며 거치는 엣지의 수를 뜻한다. 탐색하며 거치는 경로라고 생각하면 편하다.
walk의 종류	walk의 종류는 Trail, Path, Cycle, Circuit이 있다.
Trail	단순히 엣지가 반복되지 않는 walk라고 생각하면 된다.
Path	Trail의 특징을 가져가면서 노드가 반복되지 않는 구조. 시작점과 끝점이 같으면 Trail이지만 Path는 끝점 또한 겹치면 안된다.
Cycle	이름에서 짐작할 수 있듯 Trail의 시작과 끝점이 동일한 walk이다.
Circuit	Trail이지만 노드는 많이 반복되는 walk이다.

 

그래프 탐색

DFS (깊이 우선 탐색)	탐색을 진행할 때 주로 stack 자료구조를 사용하며, 재귀를 통해 구현된다. 말 그대로 하나의 온전한 경우의 수를 찾고 return하는 방식으로 구현
BFS (넓이 우선 탐색)	탐색을 진행할 때 queue를 사용하며, while문을 주로 사용한다. 모든 step을 하나씩 진행하며 완전탐색 함
특징	그래프의 모든 정점을 탐색하거나, 최단거리를 찾고싶으면 BFS 경로의 특징을 저장해야 하면 DFS를 사용하면 된다.

 

CSAPP

 

1.7.1 프로세스

프로세스란?	주 메모리에 적재된 컴파일 된 실행중인 인스트럭션의 집합
OS의 역할	프로그램이 키보드나 디스플레이, 디스크나 메인 메모리를 직접 제어하지 않는다. 이런 역할은 OS가 담당하게 되는데, 소프트웨어와 하드웨어 사이에 추상화를 담당해 I/O devices를 제어한다. OS가 수행해야 할 가장 기본적인 기능은 프로세스를 관리하는 것.
OS의 동작	OS는 프로세서를 제어하기 위한 커널을 제공. 쉘에 명령어를 입력하면 시스템콜이 이뤄지며, OS에 제어권을 위임한다. 데이터는 커널로 이동하게 된다. 커널에서는 이미 PC에 특정 메모리 주소를 전달하는 함수가 실행되고 있는데, 이 프로세서의 컨텍스트를 PCB에 임시로 저장한다. 그 후 context switching을 이용해 입력받은 프로세서의 명령을 수행 PC에 수행될 processes의 주소를 넣고 작업이 완료되면 결과값을 return하고 (여기서 processes를 처리하는 역할은 processor가), PCB에 저장되있던 프로세스를 다시 실행 그렇게 return된 작업은 I/O devices로

 

프로세스의 동작 단계를 모두 이해하는데만 3시간을 꼬박 썼다.

이제야 살짝 구조가 잡히는것같아 너무 재밌어용