CS:APP

1.7.3 쓰레드
| 쓰레드란? | 프로세스는 여러개로 나뉘어서 작동하는데, 여기서 나뉜 프로세스들은 쓰레드라고 한다. |
| 단일코어 환경 | 단일 코어 환경에서 쓰레드들을 병렬적으로 처리하는 방법은 시분할 방식으로 실행되는데, 이는 사실 완전히 병렬적으로 데이터를 처리하는 것이 아닌, CPU가 매우 빠르게 각 쓰레드를 번갈아가며 작업한다. |
| 다중코어 환경 | 다중코어 환경에서는 병렬적으로 작업이 가능하며, 각 코어가 독립적으로 쓰레드를 실행할 수 있다. |
1.7.3 가상 메모리
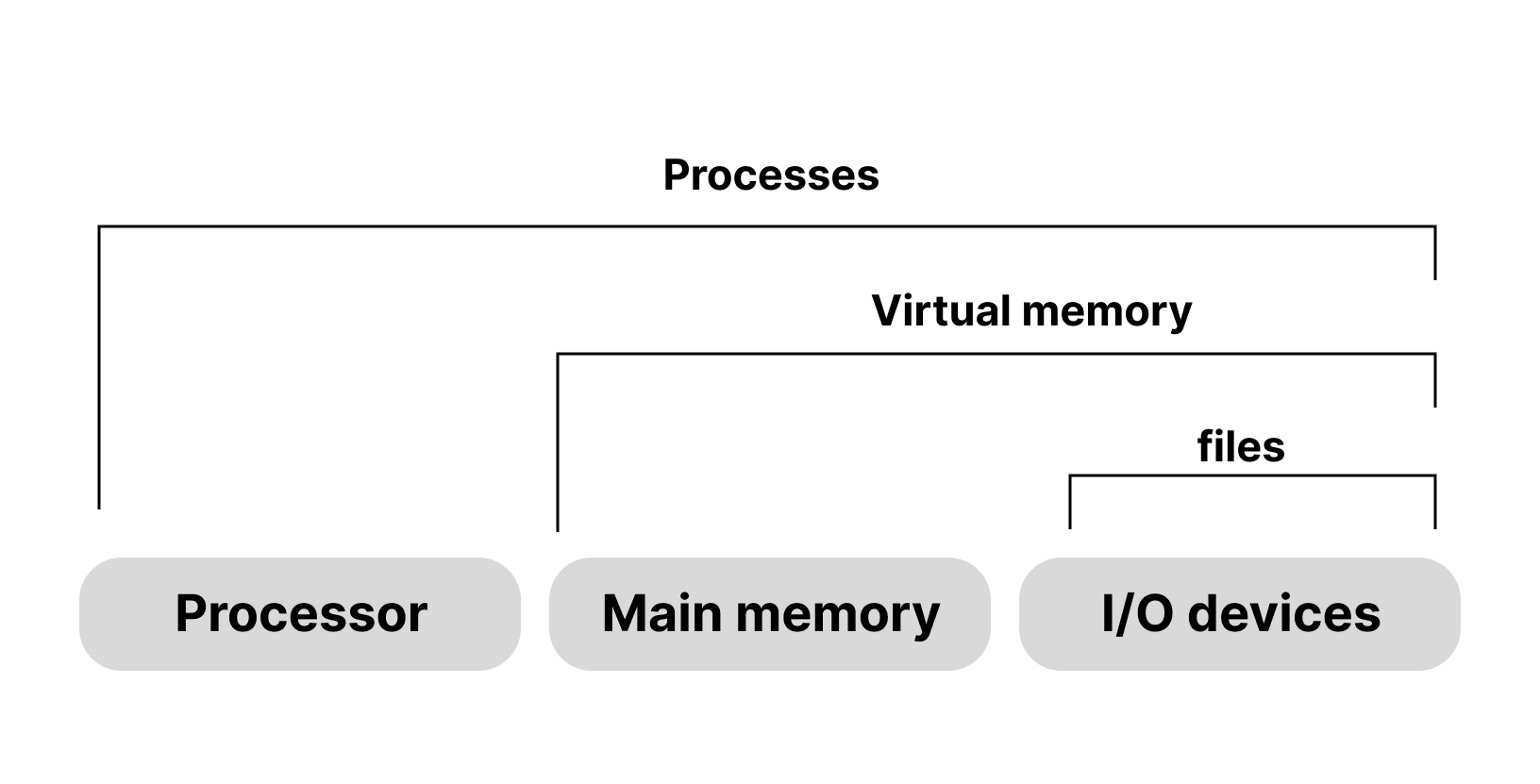
| 가상 메모리란? | 하나의 프로세서가 전체 메모리만큼, 혹은 그 이상의 주소까지 접근할 수 있게 가상의 메모리 주소를 제공하는 기술. 여기서 가상의 메모리 주소는 MMU에 의해 물리적 주소로 변환된다. 가상 메모리는 프로그램이 필요로 하는 메모리를 가상으로 제공하며, 여러 프로세스가 동시에 실행될 때 프로세스의 충돌 없이 자신만의 주소공간을 갖도록 한다. |
| MMU | 가상 메모리 주소는 MMU(메모리 관리 장치)에 의해 물리적 주소로 변환되는데, 이때 MMU는 페이지 단위로 할당된 메모리를 호출한다. 해당 페이지가 메모리에 없으면 페이지 교체 알고리즘을 사용해 현재 메모리에 있는 일부를 디스크로 내보내고 필요한 페이지를 로드한다. (나중에 아버지에게 설명을 들었는데 실질적인 메모리의 스왑은 MMU가 아닌 OS커널의 MM이 관리한다고 한다.) |
| 결론 | 이렇게 가상의 주소 + 메모리 페이징 처리를 통해 실제 Main memory의 크기보다 훨씬 큰 메모리를 요구하는 프로세서를 처리할 수 있다. |
1.7.4 ~ 1.8 파일, 네트워크
| 파일 | 파일은 있는 그대로 더도말고 덜도말고 연속된 바이트들을 뜻한다. 모든 입출력 장치는 파일로 모델링한다. |
| 네트워크 | 네트워크 또한 기다 어뎁터에서 들어오는 입출력의 일환으로, 파일과 같은 성질을 지녔다고 이해했다. 여기서 파일과 다른 점은 네트워크는 기본적으로 버퍼를 사용하기 때문에 일반적인 상황에 페이징 처리를 하지 않아도 되지만, 메모리 부족 상태에 이르게 되면 디스크의 스왑공간으로 가서 페이징 처리가 된다. |
| 결론 | 파일 = 입출력 = 네트워크 (기적의 3단논법) |
1.9 동시성과 병렬성
| 동시성 | 다수의 동시에 벌어지는 일을 갖는 시스템에 관한 일반적인 개념을 말할 때 사용. |
| 병렬성 | 동시성을 사용해서 시스템을 보다 빠르게 동작하도록 하는 것을 말할 때 사용한다. |
| 쓰레드 수준 동시성 | 최근까지 대부분의 계산은 한개의 프로세서에 의해 이루어짐 이런 구성을 단일 프로세서 시스템이라고 함 여러개의 프로세서를 가지고 하나의 OS 커널의 제어하에 동작하면 멀티 프로세서 스스템임. 최근엔 멀티코어 프로세서들과 하이퍼 쓰레딩 기법의 출현으로 일반적인 환경이 되었음. |
| 멀티코어 | 멀티코어는 말 그대로 코어가 여러개 박혀있는 구조임 각각 L1, L2 캐시를 가지고, 메인 메모리와 L3 캐시는 공유한다. |
| 하이퍼 쓰레딩 | 멀티 쓰레딩이라고도 하는 하이퍼 쓰레딩은 하나의 CPU가 여러 개의 제어 흐름을 실행할 수 있게 한다. |
| 인스트럭션 수준 병렬성 | 최근의 프로세서들은 훨씬 낮은 수준에서의 추상화로 여러개의 인스트럭션을 한 번에 실행한다. 이러한 특성을 인스트럭션 수준 병렬성이라고 한다. 사이클당 한 개 이상의 인스트럭션을 실행할 수 있는 프로세서를 슈퍼 스케일러라고 한다. |
자료구조
위상정렬

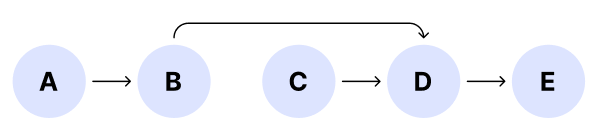
| 위상 정렬이란? | 위상정렬은 그래프가 간선(u, v)을 가질 때 u가 v보다 순서상으로 먼저 나타나도록 모든 정점을 선형으로 나열하는 것이다. 그래프가 circle을 가진다면 이러한 선형 나열은 불가능하다. |
| 위상정렬 하는 법 | 우선 BFS, queue로 정리하는 방법이 있고, DFS, stack으로 정리하는 방법도 있다. |
| BFS로 위상정렬 하기 | BFS는 기본적으로 queue를 사용하며, queue에 진입차수가 없는 첫번째 노드를 삽입하고, 해당 노드로부터 진입차수가 있는 모든 노드의 연결점을 끊어준다. 이어서 queue를 비우고, 첫번째 과정을 반복한다. |
| DFS로 위상정렬 하기 | 방문처리 되지 않은 노드를 찾는다. 해당 노드를 시작으로 DFS를 수행하는데, 그 과정은 다음과 같다. DFS 함수 내에서는 현재 노드를 방문 처리하고, 현재 노드를 시작으로 다시 DFS를 호출. 모든 인접 노드를 방문한 후에는 현재 노드를 스택에 추가. 위 과정을 모든 노드에 대해 반복한다. DFS가 완료된 후, 스택에는 위상 정렬의 역순으로 정렬된 결과가 담기게 된다. 이 스택을 역순으로 반환하여 최종 위상 정렬 순서를 얻을 수 있다. |
def topological_sort(graph):
# 모든 노드의 진입차수 계산
indegree = {node: 0 for node in graph}
for node in graph:
for neighbor in graph[node]:
indegree[neighbor] += 1
# 위상 정렬을 위한 큐 초기화
queue = [node for node in graph if indegree[node] == 0]
# 위상 정렬 결과를 담을 리스트
result = []
# 큐가 빌 때까지 반복
while queue:
# 큐에서 노드를 꺼내 결과 리스트에 추가
node = queue.pop(0)
result.append(node)
# 현재 노드와 연결된 모든 노드의 진입차수를 감소
for neighbor in graph[node]:
indegree[neighbor] -= 1
# 진입차수가 0이 되면 큐에 추가
if indegree[neighbor] == 0:
queue.append(neighbor)
# 사이클이 존재하는지 여부 검사
if len(result) != len(graph):
raise ValueError("그래프에 사이클이 존재합니다.")
return result
# 예제 그래프
graph = {
'A': ['B', 'C'],
'B': ['D'],
'C': ['D'],
'D': ['E'],
'E': []
}
# 위상 정렬 실행 및 결과 출력
try:
print("위상 정렬 결과:", topological_sort(graph))
except ValueError as e:
print("사이클이 존재하여 위상 정렬이 불가능합니다:", e)queue와 BFS를 사용해서 작업하는 방법
def topological_sort_dfs(graph):
def dfs(node, visited, stack):
visited[node] = True
for neighbor in range(len(graph)):
if graph[node][neighbor] == 1 and not visited[neighbor]:
dfs(neighbor, visited, stack)
stack.append(node)
# 위상 정렬 결과를 담을 스택 초기화
stack = []
# 방문 여부를 나타내는 리스트 초기화
visited = [False] * len(graph)
# 모든 노드에 대해 DFS 호출
for node in range(len(graph)):
if not visited[node]:
dfs(node, visited, stack)
# 사이클이 존재하는지 여부 검사
if len(stack) != len(graph):
raise ValueError("그래프에 사이클이 존재합니다.")
# 스택을 역순으로 반환하여 위상 정렬 결과 생성
return stack[::-1]
# 예제 그래프를 인접 행렬로 표현
graph = [
[0, 1, 1, 0, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 0, 1],
[0, 0, 0, 0, 0]
]
# DFS를 사용한 위상 정렬 실행 및 결과 출력
try:
print("DFS를 사용한 위상 정렬 결과:", topological_sort_dfs(graph))
except ValueError as e:
print("사이클이 존재하여 위상 정렬이 불가능합니다:", e)DFS를 사용해 작성하는 방법
최소 신장 트리

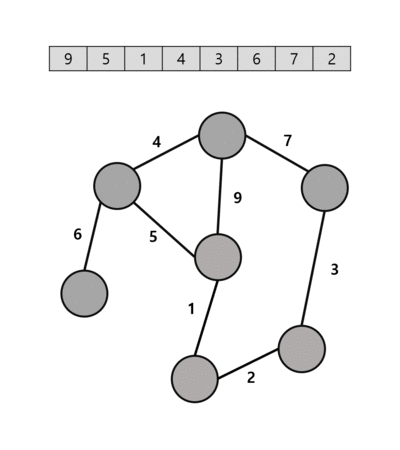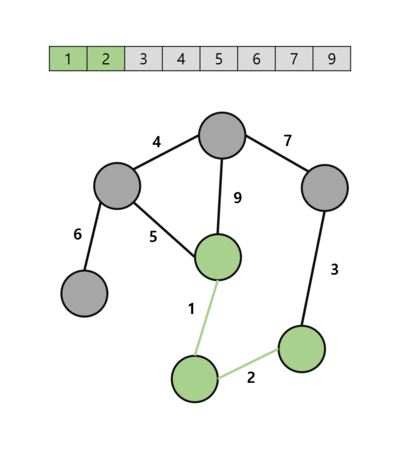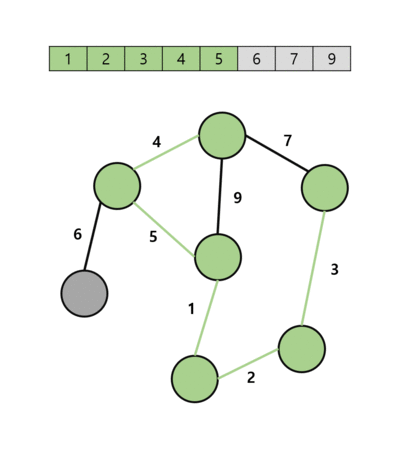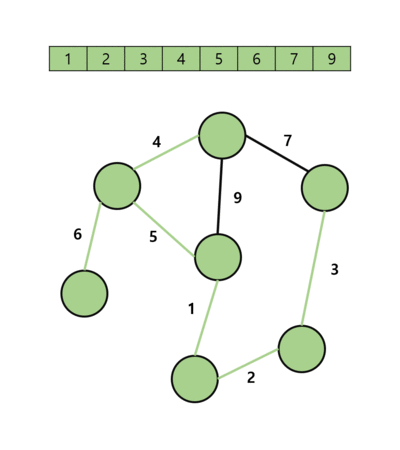
| 최소 신장트리란? | 최소 신장 트리는 그래프 이론에서 사용되는 중요한 개념이다. 주어진 그래프의 모든 정점을 포함하면서그래프의 간선 가중치 합이 최소가 되는 신장트리를 뜻한다. 사이클을 포함하지 않는 부분 그래프이다. |
| 최소 신장트리의 사용처 | 통신 네트워크에서는 신장트리를 사용해 모든 컴퓨터를 연결하고, 전기 회로 설계에서는 모든 지점을 연결하는 전선의 최소 길이를 결정하는 등의 용도로 사용된다. |
| 최소 신장트리 탐색 방법 | 대표적인 알고리즘은 프림 알고리즘과 크루스칼 알고리즘이 있다. 이 두가지 알고리즘은 각각 greedy approach를 사용해서 최소 신장 트리를 구축한다. |
| 프림 알고리즘의 탐색 방법 | 임의의 시작 정점을 선택한다. 선택한 정점과 연결된 간선 중에서 가장 가중치가 작은 간선을 선택해 트리에 추가한다. 선택한 간선으로 연결된 정점을 트리의 일부로 추가한다. 이제 트리에 포함되지 않은 정점들 중에서 트리와 연결된 간선 중에서 가장 가중치가 작은 간선을 선택해 트리에 추가한다. 위 과정을 반복해 모든 정점이 트리에 포함될 때까지 진행한다. |
| 크루스칼 알고리즘의 탐색 방법 | 모든 간선을 가중치 순으로 정렬한다. 정렬된 순서대로 간선을 확인하면서, 사이클을 형성하지 않으면서 최소 가중치 간선을 선택한다. 선택한 간선을 최소 신장트리에 추가한다. 위의 과정을 반복하여 모든 정점이 연결될때까지 진행한다. |

트라이(Trie)
| 트라이란? | 트라이는 검색트리의 일종으로, 키가 문자열인 동적 배열 또는 연관 배열을 저장하는데 사용되는 자료구조이다. |
| 어디에 쓸까 | 문자열을 효율적으로 저장하고 검색하는데 사용되며, 특히 문자열 검색에 대한 자동완성 기능이나 문자열 패턴 매칭등에 유용하게 활용된다. |
| 트라이의 작동 구조 | 각 노드는 한 문자를 나타내는 라벨을 가진다. 주로 알파벳 문자열을 다루는 경우에는 각 노드가 알파벳 하나의 문자를 나타내며, 노드의 자식은 해당 문자 뒤에 오는 다음 문자를 나타낸다. 생각보다 구현하기 쉽다. |
다익스트라, 플로이드 와샬
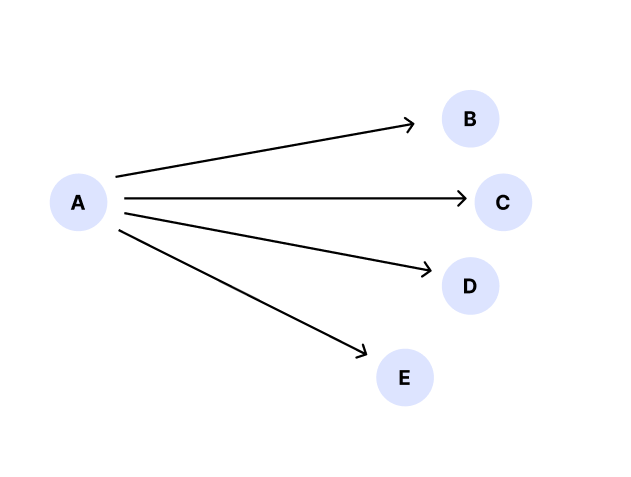

| 다익스트라 | 하나의 정점에서 출발했을 때 다른 모든 정점으로 최단 경로를 구하는 알고리즘이다. |
| 플로이드 와샬 | 모든 정점에서 다른 모든 정점으로의 최단 경로를 구하는 알고리즘이다. |
infinity = float("inf")
def make_graph():
# tuple = (cost, to_node)
return {
'A': [(10, 'B'), (30, 'C'), (15, 'D')],
'B': [(20, 'E')],
'C': [(5, 'F')],
'D': [(5, 'C'), (20, 'F')],
'E': [(20, 'F')],
'F': [(20, 'D')]
}
def dijkstras(G, start='A'):
shortest_paths = {}
unvisited = dict.fromkeys(G.keys())
for node in unvisited:
shortest_paths[node] = (infinity, None) # (최단 거리, 이전 노드)
shortest_paths[start] = (0, None)
while unvisited:
min_node = None
for node in unvisited:
if min_node is None:
min_node = node
elif shortest_paths[node][0] < shortest_paths[min_node][0]:
min_node = node
for edge in G[min_node]:
cost, to_node = edge
new_distance = cost + shortest_paths[min_node][0]
print(new_distance)
if new_distance < shortest_paths[to_node][0]:
shortest_paths[to_node] = (new_distance, min_node)
del unvisited[min_node]
return shortest_paths
def print_shortest_path(shortest_paths, start, end):
path = []
node = end
print(shortest_paths, start, end)
while node is not None:
path.append(node)
node = shortest_paths[node][1]
if path[-1] == start:
print(f'Shortest path from {start} to {end}: {path[::-1]}')
else:
print(f'No path from {start} to {end}')
def main():
G = make_graph()
start = 'A'
end = 'F'
shortest_paths = dijkstras(G, start)
print_shortest_path(shortest_paths, start, end)
main()다익스트라 알고리즘으로 최단경로를 역추적하는 코드
'Krafton_Jungle > Study' 카테고리의 다른 글
| Krafton_jungle 5기 14일차 TIL - 알고리즘 문제풀이 (0) | 2024.03.31 |
|---|---|
| Krafton_jungle 5기 13일차 TIL - B-Tree, 알고리즘 (0) | 2024.03.30 |
| Krafton_jungle 5기 11일차 TIL - 알고리즘 시험, 그래프 자료구조, CS:APP (0) | 2024.03.28 |
| Krafton_jungle 5기 10일차 TIL - 알고리즘 문제풀이, CS:APP (1) | 2024.03.27 |
| Krafton_jungle 5기 9일차 TIL - 알고리즘 문제풀이 (1) | 2024.03.26 |
